Part 1: The Question
This rather innocuous looking question came at the end of one of our GCSE mock exams and at first glance didn’t seem like it would cause to many problems. Part a is simple enough but part b was basically unlike any question I had seen at GCSE – definitely not a question I had adequately prepared my students for. The marksheme doesn’t even reveal the true glory of this question

Every attempt to explain this question to students led to whiteboards full of confusion. So with the help of some wonderful colleagues we created some resources to help actually teach the skills required to achieve these few marks.
Part 2: Equating Coefficients

We couldn’t find any resources for teaching equating so we decided to create one ourselves. We created a worksheet using the principles of the “Slow Build” where students slowly work through examples starting from examples they have seen before and getting progressively more difficult. Also always a shout out to Craig Barton and VariationTheory who I have big time fan girled over ever since I sat next to him in a session at BCME 2018. It felt fun to use the idea of collecting like terms – something that the students were very comfortable with – to explore a much deeper method.

Working in pairs the students were able to carefully work through all the questions with minimal input from me – drawing a few students to our glorious whiteboards when they were in need of a nudge.

The use of examples they recognized helped with the transition to more tricky and interesting questions on cubics later on an fed in nicely to our work with cubics (details in a future blog post)
Once I felt confident that the students were comfortable with the ideas behind equating coefficients we moved on to the main event (in a different lesson)
Part 3: Getting to the problem

Working out that this problem was relevant to our initial question was such a wonderful aha moment for me. We were just playing around on some whiteboards wondering what the simplest form of the vectors question might look like – a classic problem solving technique that always brings me joy – when we settled on this. Although you can solve this with similar shapes as well as straight line graphs (I will leave those as an fun extension) the vector proof feels not only very elegant but also leads directly into its more harder variations. Below is how it was presented to the students after some discussion and attempts from them.

Once the students had attempted this question we worked through it together as a class making sure that there was a consensus of understanding they were then encouraged to work through the rest of the worksheet in pairs using the whiteboards around the room to play around with the questions.
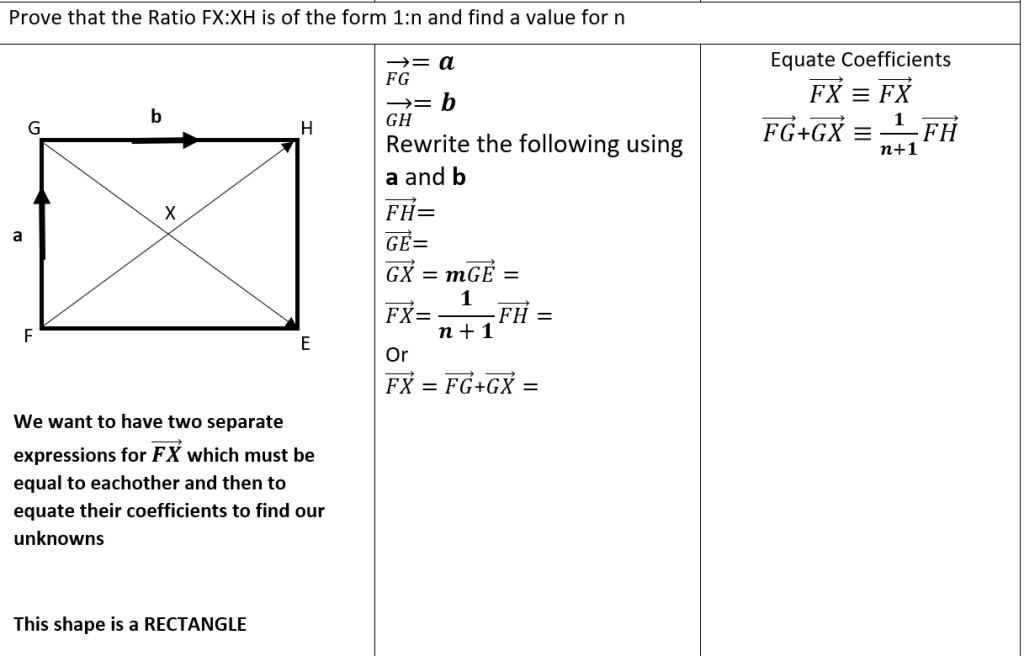
Eventually they had tackled a few simpler questions and they were faced with the same (albeit more structured) vectors question they had seen in their mock exam.

Part 4: The Main Event
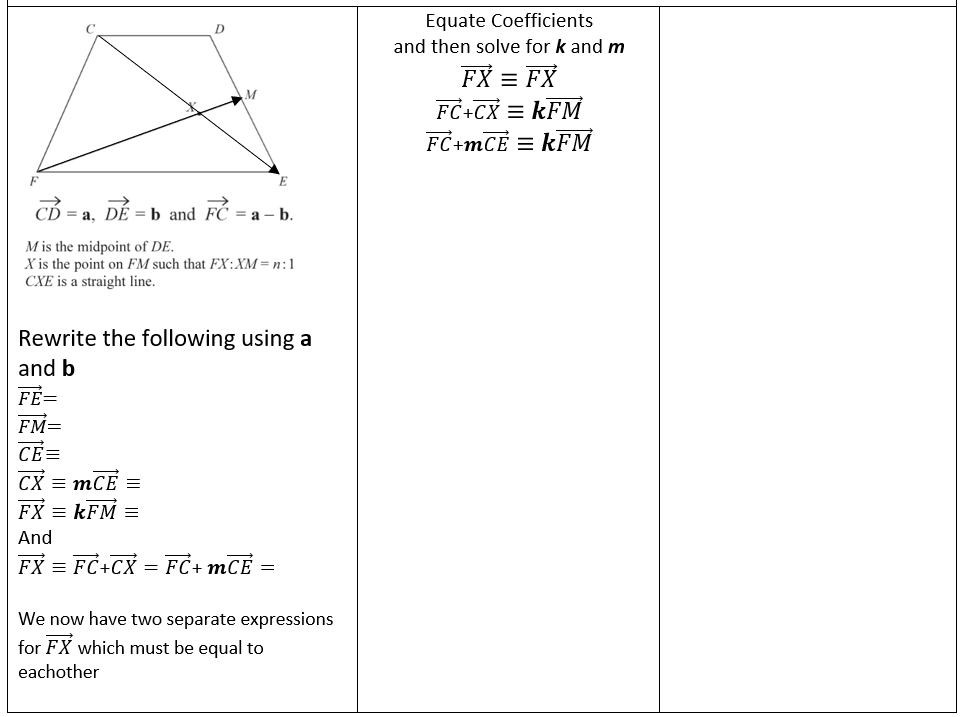
Seriously this was two marks or something. The students could have completely left this out and still done phenomenally well (as they did!) but the students have every right to want to understand everything that could possibly come up on their GCSEs and also maths is so cool and the JOURNEY. The JOURNEY. Such an absolutely joy. Big shout outs to the one student in the whole year group who got the marks as well as to some awesome colleagues for dealing with me pestering them about the question repeatedly over the course of a week.
Part 5: AOB
Whether a question like this will every actually come up again seems very doubtful, and whether my students would have thought to use these skills if it had come up is also doubtful but I think there is such a joy in deeply exploring one question and seeing all the other Maths that falls out.
Below are the links to the full worksheets – feel free to click, download and try them yourself!
If you are interested in seeing more Slow Build worksheets I am currently in the process of adding them to the Slow Build page on this website!
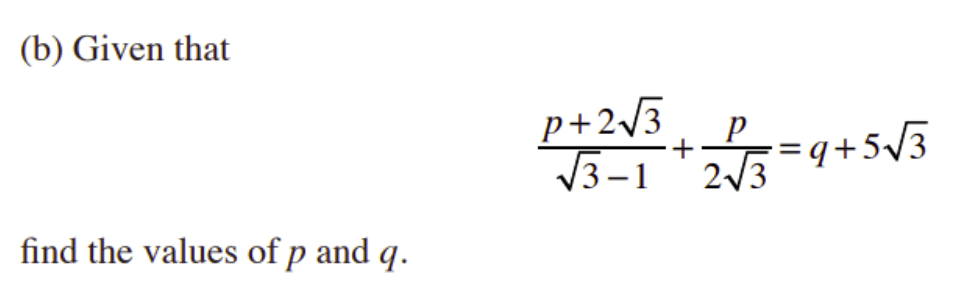

NJK

You must be logged in to post a comment.