
The wonder of the UKMT
I have said before on this blog that I absolutely adore the UK Maths Challenge as a way of massively improving your problem solving skills and using preexisting tools in totally new ways. It’s also an absolute goldmine for interesting purposeful practice. One of my favourite way of creating resources is by choosing a UKMT (UK Maths Trust) question that I particularly enjoy and seeing in what glorious directions it can lead.
From Question to Exercise: Square Root Puzzle
Lets look at the question above – what seems like a relatively simple question has a wonderfully elegant solution. I will include the answer at the bottom of the post – although as usual I would recommend trying the question first!

So to start with students are encouraged to just try the question themselves – they have the whole page to write down their thoughts and try different things and if they want some support they can turn to the next page.
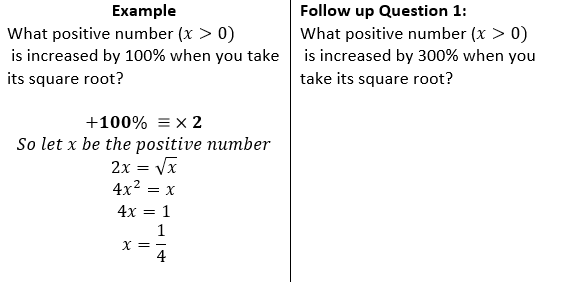
They can work through the simpler example I have given them and then go on to doing very similar questions to the original so they can practice the steps involved. These slight variations mean that students can use what they have used in previous examples to help when the questions get slightly weirded!
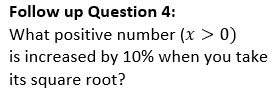
The questions progress, using an differing increases before finally looking at a more general example!

But why?
Although the question feels pretty niche there is lots of maths to be practised here. The link between a percentage increase and the corresponding numerical multiplier, solving simple quadratic equations and some nice thoughts on fractions lead to an exercise that practises some key skills in a nice creative way! I plan on using it as some problem solving practice after having taught part of those topics.
Please feel free to try it by downloading here – The answers are available through the resources under the subheading “Problem Solving”
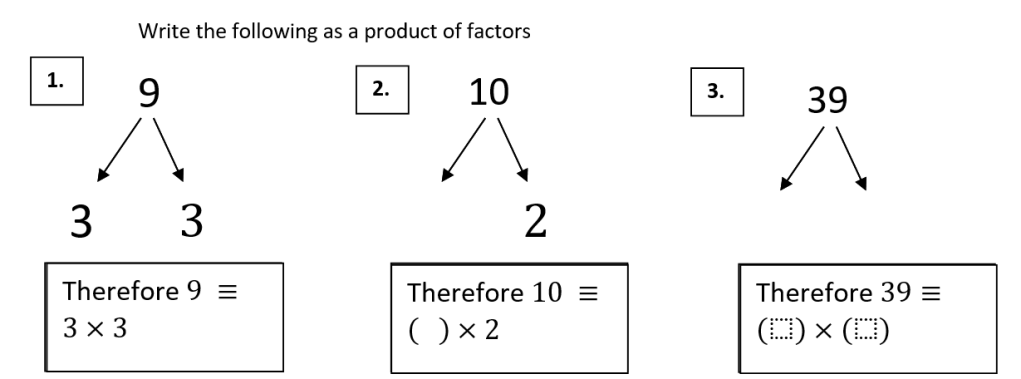
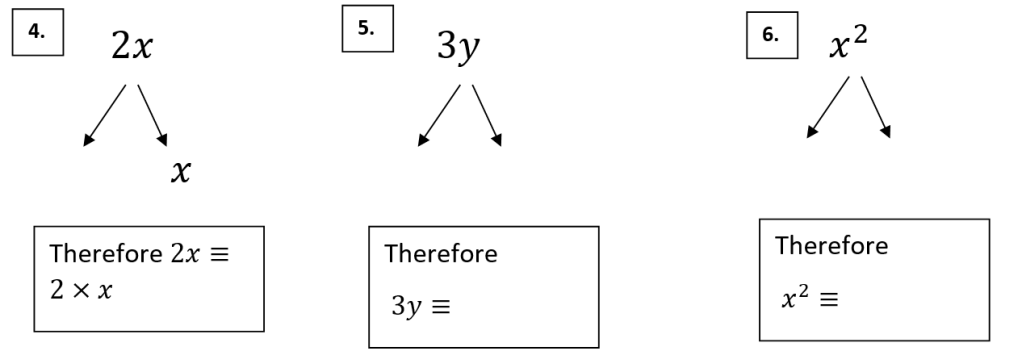
From Question to Exercise: Factors and Square Numbers

How would you attempt the above question? You could just work out the multiplication and then square root that product to find out the missing value. But square rooting in notoriously a tricky function without a calculator and also where is the fun in that! It also will become an increasingly impractical method the larger the numbers get – for example in the question below…
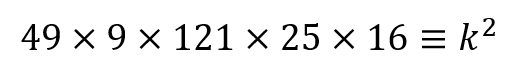
Simplifying the question

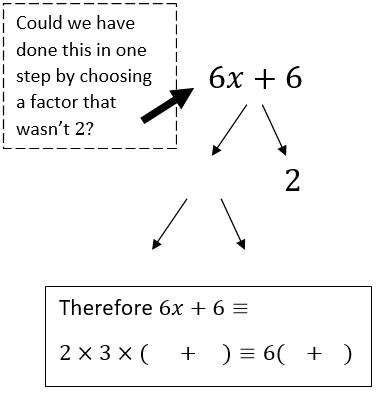
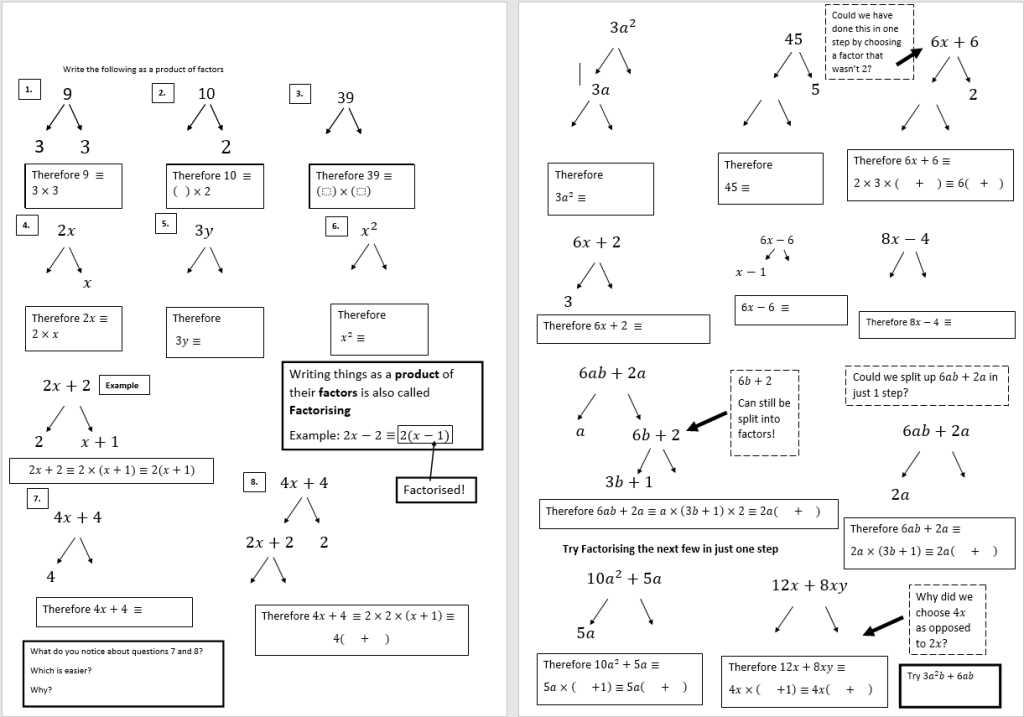
As with lots of the worksheets I make I like to start with simple questions for students to work through and throwing in an example to help but the aim is for it to be a relatively self-explanatory exercise that slowly builds to the intended questions that we want to solve!
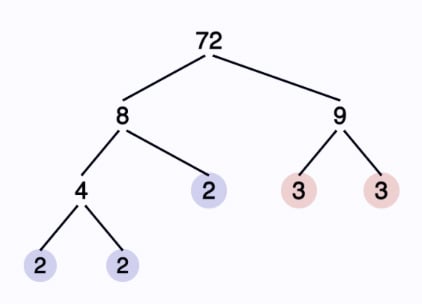
These questions also came from a wonderful UKMT question that I saw and needs some knowledge about the structure of square numbers to answer it. In particular that the prime factors of square numbers have to come in even pairs. For example 16 can be represented as 4 x 4 but also as two pairs of 2 x 2. The number 18 on the other hand is built from 3 x 3 x 2 so you have a pair of 3s but then one factor left over so it is not a square number. How could we make 18 a square number just by looking at its factors? We need to find a buddy for that extra factor of 2 so by x 2 we end up with 3 x 3 x 2 x 2 = 36 which is a square number! You can even rearrange it slightly and write it as (3 x 2) x (3 x 2) to make it even clearer that it is a square number as it is something times itself.

So for the question above you can rewrite 64 as 8 x 8 and 4 as 2 x 2 and by rearranging you then have (8 x 2) x (8 x 2) which means that 64 x 4 has to be 16 squared! A wonderfully simple way of solving these questions and also a great excuse to practise factorising (prime and not prime!)

You can try the worksheet yourself here and the answers can be found on our resources page. Its such a delightful little puzzle with a lovely solution – Even coming up with your own questions is fun so I implore you to try that too!
Post Credits
The UKMT is an absolute goldmine of maths and puzzles. Even more excitingly the UKMT has extended solutions to their maths challenges that include additional questions and investigations for each question so I would definitely suggest checking that out here
Below is the solution to the original problem:

As always thank you so much for reading and if you are interested in getting involved with us let us know here and you can also subscribe so you don’t miss out on any content by entering your email below!
NJK

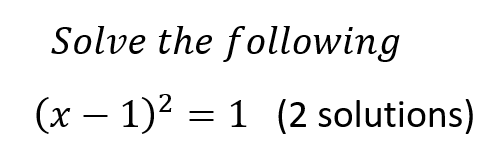
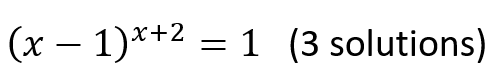

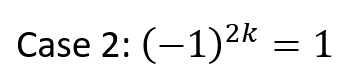
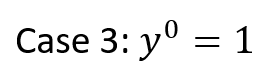







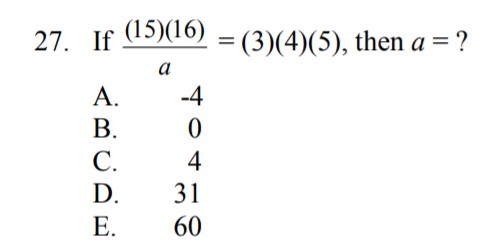




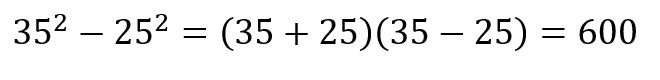





























You must be logged in to post a comment.