
Asking “What is Factorising?”
The majority of the time, when I hear this question asked in class I have heard the word “Brackets” come up in the response. As a teacher when I hear this answer I generally take it as correct – The student has clearly remembered part of the method behind factorising and is stating a key symbol they use during that process. But there would usually be silence when I asked how factorising related to its root – Factors. What are the factors of 3x+3 – why does it feel strange to describe (x+1) as a factor?
Using a Factor Tree to Practise Factorising
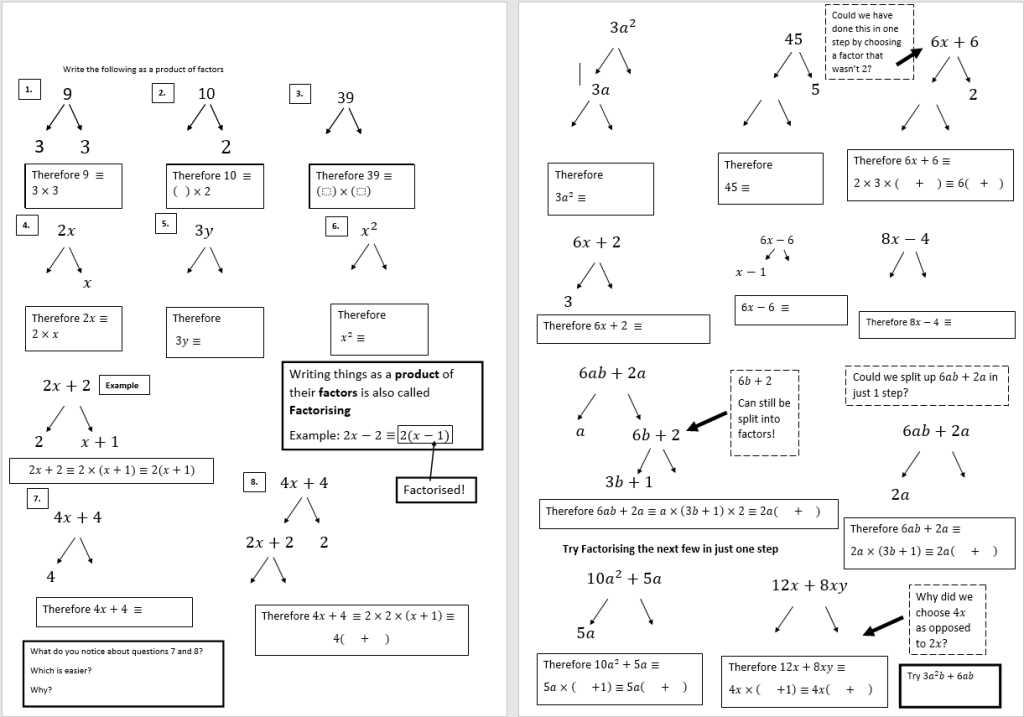
When students are taught to write numbers as the product of their prime factors we tend to use a “tree” to split the numbers (As shown below)
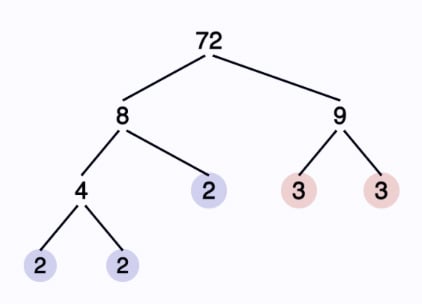
I decided to see if I could use this same method to practise students ability to factor expressions as well and then create a link between what you are doing in both case – Splitting something into a product of their factors.
So I made a worksheet and gave it to my students to see what they would make of it. As the sheet contains a lot of structure I let them initially work through it in pairs and without giving them too much introduction so that they could do all the thinking themselves. Before this lesson we had previously practised how to factorise different simple linear expressions (Using the worksheet here) so we had already seen and discussed some of the maths behind expanding and factorising expressions.
The Worksheet
(The worksheet is attached here – I encourage you to try it yourself before continuing!)
The purpose of the worksheet is for students to recognise that when they are factorising the parts they have inside and outside the bracket are the factors of the expression. Intuition that will help with many similar problems later in their mathematical careers.
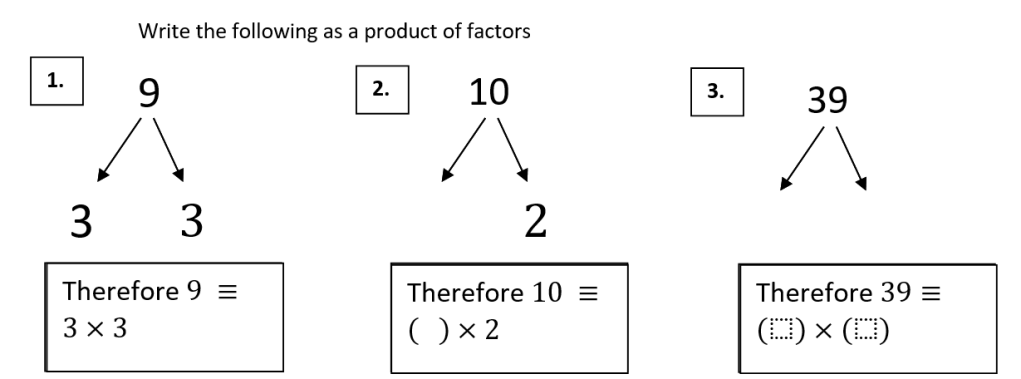
The sheet uses the idea of a “Slow Build” to get students to start from something they are comfortable with and slowly build to deeper questions
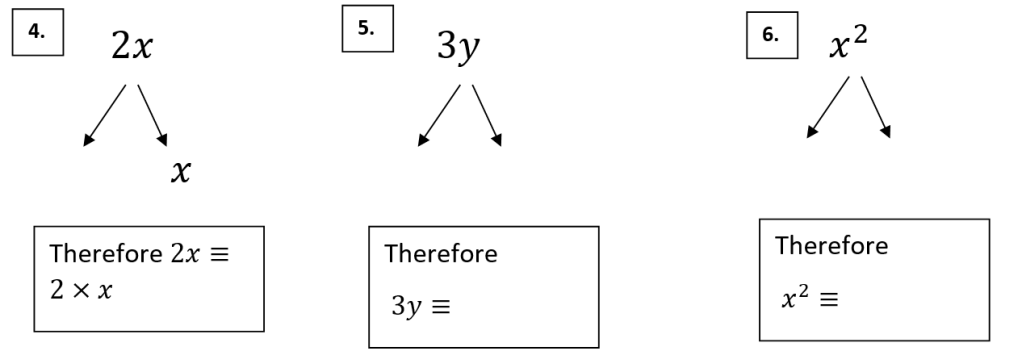
After quickly discussing questions 4 – 6 with the class they were then left to attempt the rest of the worksheet while I circulated to check on progress. The sheet contains various questions and hints that students are required to write an answer for which lead to some fantastic discussion throughout.

The rest of the worksheet contains more practise including looking at harder examples eventually moving to expressions with multiple variables that they hadn’t seen before (Although in the context of this worksheet were answered quite successfully!)
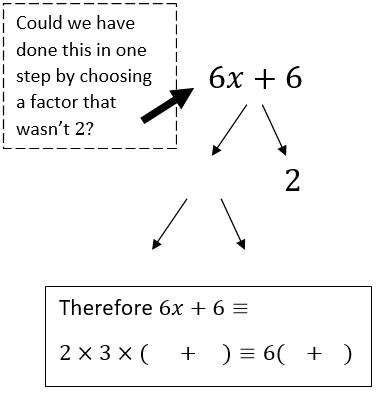
This Question on the left gets the students to ask if there is a more efficient way of answer the same question leading to a factor of 6 on the outside of the bracket later on. As a class we discussed the differences between prime factorisation and splitting things into their factors and also using brackets when writing something in its factorised form. This question on the left encapsulates lots of these thoughts at once.
Factor(is)ing
I am undecided as whether I like using the word Factorising when looking at products of factors or whether I prefer the more american Factoring. The (is) in Factorising feel slightly unnecessary and Factoring seems to convey just as simply that we are going to be looking into factors. Let me know which one you use!
Post Credits
Overall this worksheet created some very interesting discussion with my students and also led to increased fluency when dealing with factoring questions in later lessons. The idea that factors can also be algebraic expressions and not just integers was also a great source of conversation in the classroom during the lesson.
I have included an image of the whole worksheet below in case you are unable to view the download. Answers are available through the Resources page.
Thanks for reading!
NJK


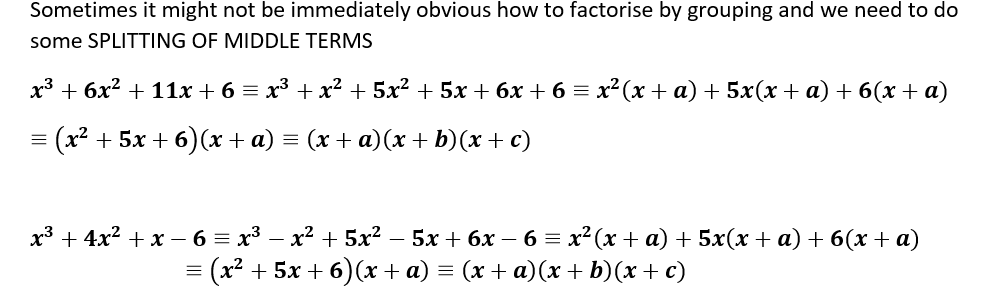

You must be logged in to post a comment.