Author: Samuel Davies

Farmers’ Area Problems

I recently came across this fencing problem posed by two mathematically minded farmers, the first part of which I feel is rather well known. Questions such as these are easy to visualise, meaning you can often give an instinctive answer and then test if your intuition was correct after solving the problem.

Part 1: The Warm Up

Consider an established farmer who has a very long (infinitely, if need be) straight fence forming part of the boundary of a field. Generously they have allowed you to use this fence, while constructing your neighbouring plot of land. Therefore we plan to enclose a rectangular field, only needing to build 3 sides of the quadrilateral. We will stipulate that the maximum length of these 3 sides is a length of L. The neighbours fence is shown below, on the left vertical.

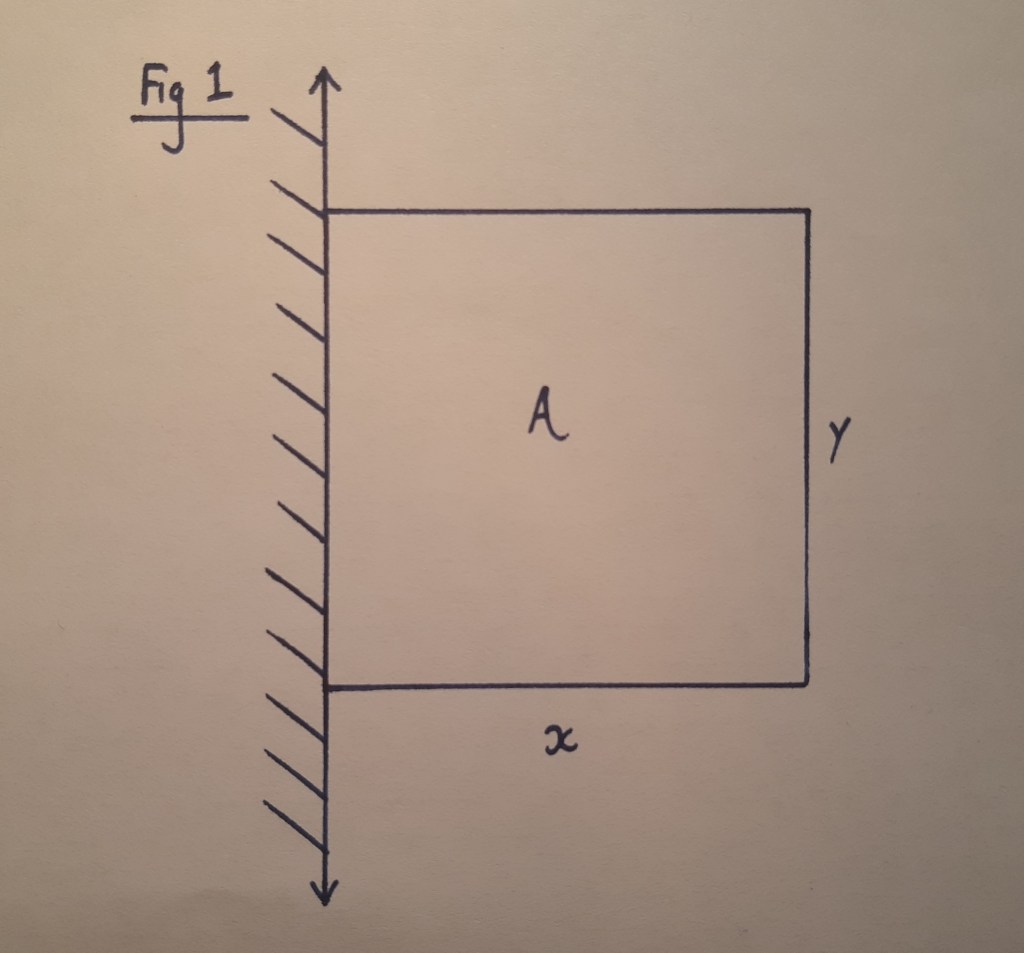
Question: Using a fence of total length L, what ratio of sides will give the maximum area?

The idea here is to use the constraint on the fence length L to create an equation using our unknown side lengths, x and y. We can then use this to create a formula for the Area, using the constant L and one unknown.

With this formula in place, the problem then becomes a question of maximising the equation, which we can achieve by finding the stationary point of the derivative.

I’ve solved this below, so don’t scroll down if you would like to try this yourself!

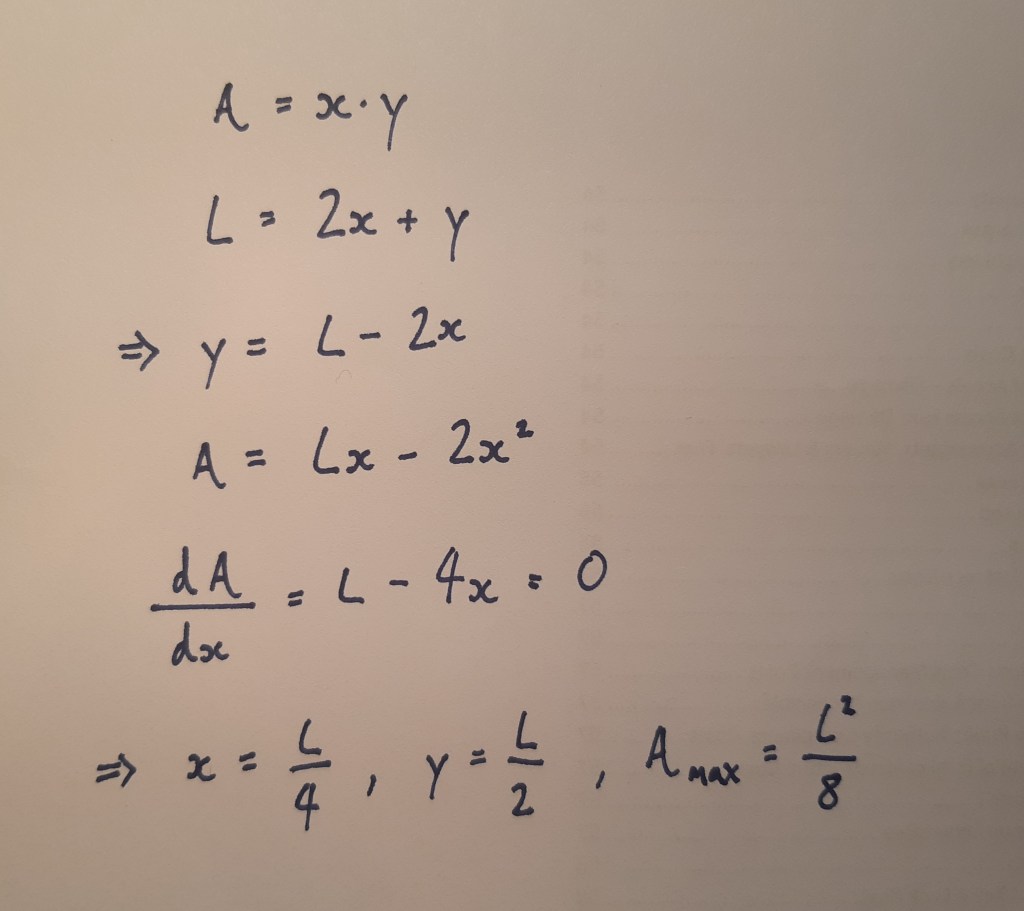
I’ve also created a Desmos Graph to see how the area changes with different values of L.

So the answer is a 2:1 ratio in the direction of the neighbours fence. While this may not have been your initial intuition, it follows that adding to the fence in the vertical direction only costs half as much as adding in the horizontal direction, due to the free fence offered by our neighbour. Therefore, the maximal area will be achieved by having a vertical length double that of the horizontal length.

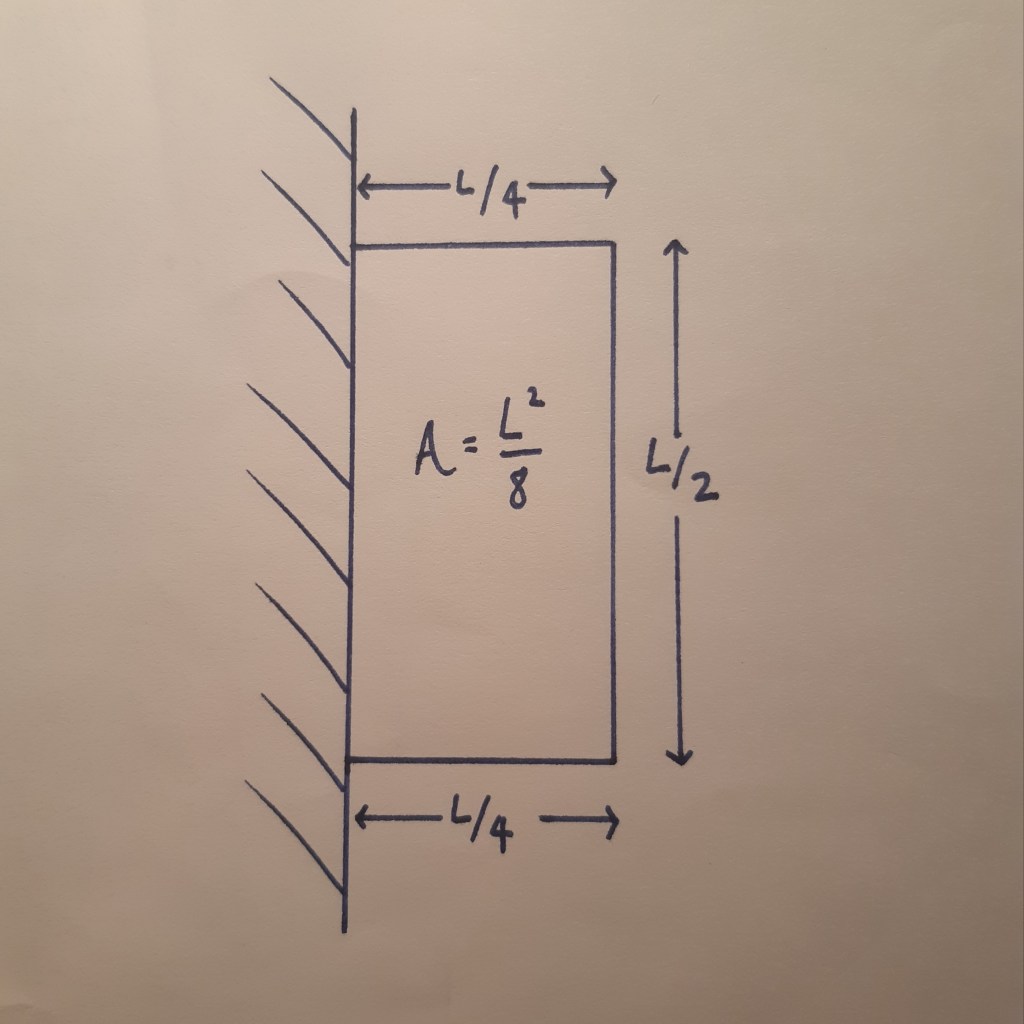
We will leave how our generous neighbour tends to their field of infinite size to another day.

Part 2: The Main Event

Considering the success of the first project, we have decided to expand our farm by building a new fence for a new field. This time the plot of land is somewhat different. 

In this case we have a square farm building in the middle of another very large field. We’ve realised that if we include the edge of the building as part of the fence, we can increase the area we enclose. 

One option is to align the field with the edge of the farm building (shown on the left below). However, our established neighbour has suggested we might want to consider using the long diagonal of the building as part of the fence. These two scenarios are shown below for the vertical and diagonal configurations building.

Question: Again considering a total fence length L and a square building of length l in both scenarios, which configuration gives the maximum area?

Again the solution to these two configurations follows a very similar pattern to the warm up question above. However, instead of working out the ratio of the side lengths, we need to find the maximal area of each scenario.

In the interest of time, we will solve these in parallel as the solutions are very similar. Additionally, there is a neat trick that we can use to minimise the effort required. In opening two statements, we can observe that both equations have equal coefficients of x and y. Therefore, we can interchange x and y freely in the formulas (since they are variables we have made up to understand the problem). This means any solutions we find for x, is automatically valid for y and is called a symmetric argument.

Now all that remains is to determine which of the two areas in the final row are larger. If we assume that the vertical configuration yields a larger area than the diagonal configuration, we can create an inequality to simplify in terms of L and l.

So we have found that the relative lengths of the fence and the side of the building impact what choice we should make. If the fence is much shorter than the side of the building, then we should choose the vertical configuration. Of course, we can reverse the inequality to find the alternate scenario.

Again, I’ve created an interactive Desmos Graph that gives a visual interpretation of the problem.

With the two solutions in place, we can now compare against our original instincts to check if we were correct. If you were, well done! If, like me, you were not, I find it useful to examine to think about why my intuition failed in order to improve for next time!

And finally, as the old saying goes, the enemy of my enemy is my fence.

SED