The problems:
These three seemingly very different questions all showed up in the same SMC paper in 2017. Try each one yourself and see if you can work out what one trick links them all together!
DOTS: A Party Trick
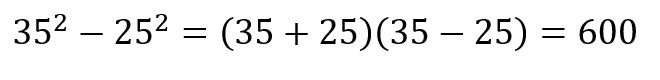
I’ve always been thrilled by the ability of using the “Difference of two squares” to simplify problems. Whether its answering numeracy problems quickly and easily like the one above or using it to crack open harder problems like the three SMC problems above.

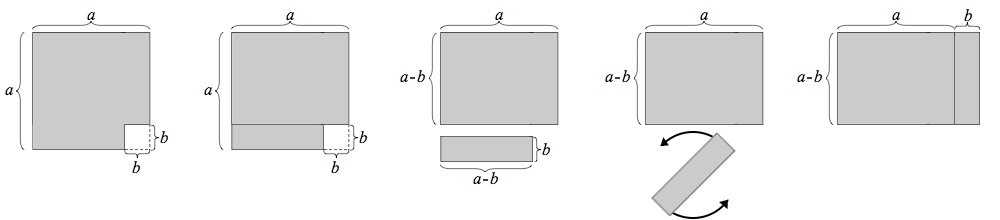
At the bottom of this post I will include some worksheets (not made by me) that practice using this skill in simple and fun ways as well a lovely geometric proof of the above formula. There will also be some extension questions as well as seeing how these techniques show up in the A level curriculum.
The Answers:
Puzzle 1:

This question is a great example of just starting off trying to simplify your answers and seeing what pops out. Looking at the multiple choice options available here its not immediately clear how any of those could possibly be the correct answers.
The most interesting part of working through this is when you get to the following step ![]() Recognising that by definition 1 is a perfect square means that whenever you have a square number mius one you can use this formula. This give you the final piece of the puzzle which simplifies to answer E as shown below. Such a elegant question!
Recognising that by definition 1 is a perfect square means that whenever you have a square number mius one you can use this formula. This give you the final piece of the puzzle which simplifies to answer E as shown below. Such a elegant question!

Puzzle 2

This one has a longer but no lesson elegant solution. There are plenty of ways to solve this one but the words “The difference between the squares of their ages” should immediately get the DOTS alarm bells ringing. Using DOTS simplifies this problem down in a lovely way and makes the algebra much more manageable as the answer below shows.

There is also some extension to this question which are a great way to practise the skills yourself – try them yourself and contact us if you have questions/answers!

Puzzle 3: The finale

It is not immediately clear how DOTS could help you with this question. The first thing to say is that the main reason I thought to use this trick is simply that I have answered lots of problems before. There is no substitute for practise and increasing your mathematical toolkit but playing around with lots of different maths. Needing almost any excuse to use DOTS and additionally y squared in the question meant that I went down that route first of all.
I’m not going to go over every step of the question but the step where you set each bracket to different factor pairs of 15 is not an easy step to see – once again there is no replacement for practise and seeing this question will help with similar questions in the future – I will also include an A Level question that uses this exact technique later on.

Honestly an absolutely glorious question. It is no surprise that it is one of the last questions in the Senior Maths Challenge (For school years 10+) when it requires lots of quite difficult techniques (also under a timed exam pressure! Very tricky!)

Bonus A level question:

This A level question is a lovely way of seeing how theses skill show up in the school curriculum and are a great way to prove some seemingly not straightforward mathematical statements. Try it yourself! I have attached a link below to a document with a group of these questions and importantly the answers to them.
Post Credits
Difference of two squares is a wonderful trick that has a multitude of problem solving uses. The more problems you do and the more you can recognise this the easier (and more fun!) these questions will become.
I have included below a link to worksheets created by the legend Don Steward that can help you practise DOTS in numerical settings.

If you have any extra thoughts/questions please do send us a message and we will get back to you as soon as we can!
NJK



You must be logged in to post a comment.