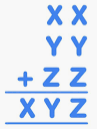
I was recently given this problem by a colleague and it immediately took my interest. As soon as I saw it my first thoughts were not “what is the answer?” but “is there an answer? Is there more than one answer? Can I prove this?”.
I spent that lunchtime in my classroom looking at the problem. I started by looking at the digits in the units column and noticed that since the value of the units in the answer must be z then x + y = multiple of 10. This gave me different possibilities to consider:
- x + y = 0. Since x or y can not be negative (they are digits) then the only other possibility is if x = y = 0 and using quick inspection this clearly does not work.
- x + y = 10. This is feasible since there are multiple ways 2 single digits can sum to 10.
- x + y = 10n, where n is any integer greater than 1. This is not possible since x and y are single digit numbers so can not sum to any number greater than 18.
This was the first breakthrough in the problem as I now had an equation that places a constraint on the possible values of x and y.

I then adopted a similar approach with the tens column (x + y = 10 so don’t forget to “carry” the 10 into the tens column which I initially did!). Looking at the digits we can see that 10x + 10z + 10 = 100x which we can simplify to get z + 1 = 9x. Now since x, y and z are all single digit numbers I could then use the two constraints to deduce their values:
x + y = 10 (A)
z + 1 = 9x (B)
- Looking at equation (B) x = 1 and z = 8 since x, y and z are single digit numbers
- Substituting x = 1 into equation (A) we can see that y = 9
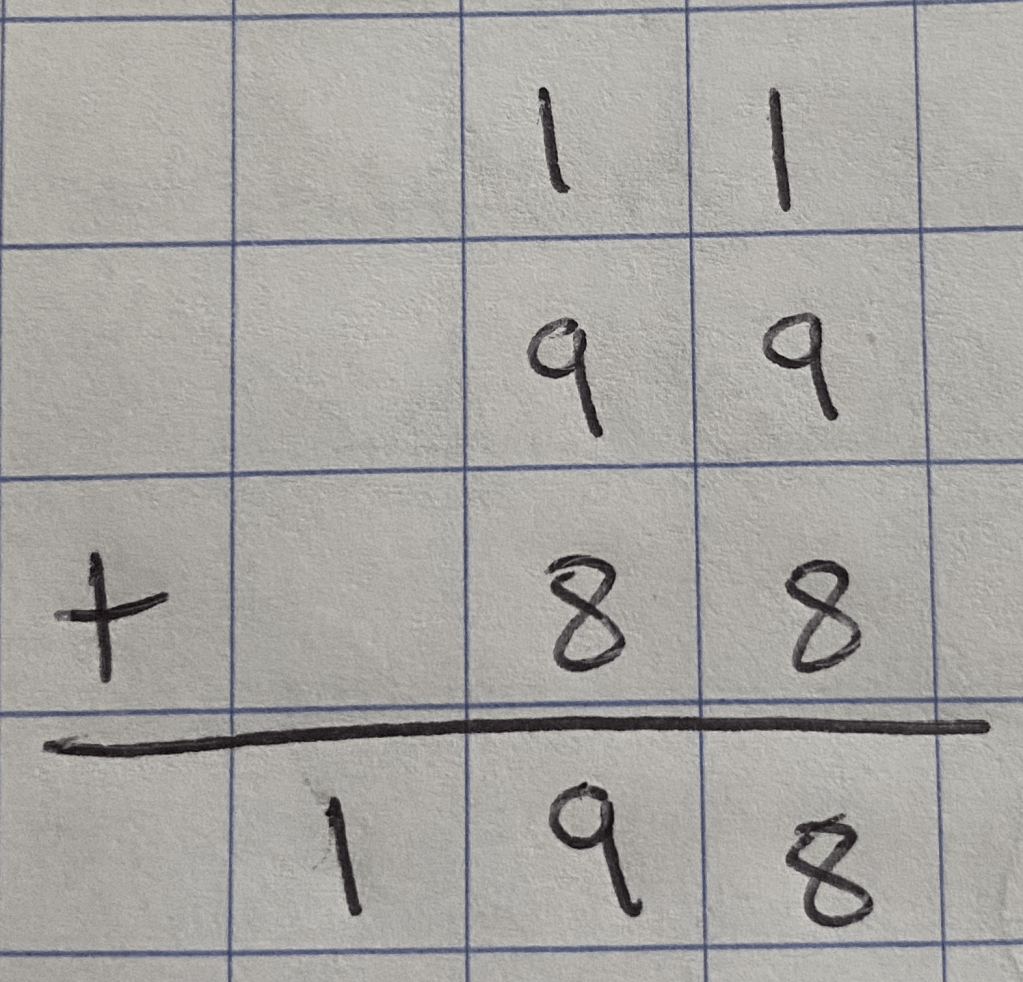
So I had obtained “the answer” and could see that it works. It’s always satisfying to find the answer to a maths problem but it’s even more satisfying to say with confidence that this is the only answer and prove it with reason. I presented this problem to a high ability year 8 class with no instructions and was intrigued to see how their thinking was to trial numbers and simply search for “the answer”. As expected, many of them were able to find the correct values for x, y and z but weren’t able to tell me with any conviction if these are the only possible answers.
I am sure there are other proofs to this relatively straightforward problem and I would be interested to see people’s suggestions!
DTH
You must be logged in to post a comment.